How Virtual Addressing Works
Oct 21, 2018 13:52 · 1748 words · 9 minute read
Operating systems manage many physical resources and provide nice software APIs on top of them so that you and I can easily write code. One of those resources is RAM. Physical RAM itself is fragmented and limited and therefore hard to manage. For example, not all physical RAM addresses are available for use (some map hardware devices, while others are reserved for the processor). Operating systems also provide an abstraction of processes, each of which have their own isolated view of memory. This would be quite complicated if the OS were constrained to just giving out physical RAM. In order to simplify the implementation, the concept of virtual addressing was introduced. In this post, we will explore how x86-64 (64 bit) virtual addressing works.
64 bits of address space could theoretically represent 2^64 bytes, or 2^24 terabytes. Suffice it to say, no machine (or program) any time soon will ever need that much RAM. So, the virtual address space is only 48 bits (although Intel has recently introduced 57 bit virtual addresses). This means, we have 256 terabytes of virtually addressable RAM. So, what happens to the top 16 bits of the address? These must be a sign extension of the 48th bit (i.e. if the 48th bit is 1, the top 16 bits must be 1; same for 0).
Since ultimately memory needs to be backed by physical RAM, there needs to be some way to convert from a virtual address to a physical address. For that, the operating system uses structures called page tables. One page is 4096 (or 2^12) bytes (there are larger pages which we will get into later). One page is the smallest unit with which physical RAM is given out (e.g. even if your process just wants one byte, an entire physical page will be allocated for it).
We will discuss paging with 4 levels of page tables (although intel has recently released 5 level paging). The 4 levels are referred to as the page map level 4 table (PML4), page directory pointer table (PDP), the page directory table (PD), and the page table (PT). For simplicity, we will refer to the levels as L4, L3, L2, and L1 respectively.
Each level can be thought of as an array of 512 64 bit integers (conveniently, this is 4096 bytes, or exactly one page). Each integer is considered an entry, where an entry is defined bitwise as follows (some fields ommitted for brevity):
| Bit(s) Idx | Description |
|---|---|
| 0 | Present? |
| 1 - 6 | CPU specified |
| 7 | Huge page? |
| 8 | CPU specified |
| 9 - 11 | OS specified |
| 12 - 51 | Page aligned physical address shifted down 12 bits (which are all 0s) |
| 52 - 62 | OS specified |
| 63 | CPU specified |
One thing to note is that the physical address is 40 bits, which means there can be at most 2^40 pages, or 4 petabytes of addressable physical ram.
In the L4, L3, and L2 tables, the page aligned physical address points to the top of the next level table. In the L1 table, the physical address points to the actual physical page backing the virtual address.
The 48 bit virtual address is broken up into 4 chunks of 9 bits and 1 chunk of 12 bits. The four 9 bit chunks are indices into the 512 entry page tables described above. The 12 bit chunk is an index into the physical page. Let’s demonstrate this with an example. We will represent the 48 bit virtual address in octal (i.e. digits from 0-7) since 3 octal digits are 9 bits and 4 octal digits are 12 bits.
Imagine we have the 48 bit virtual address 003 010 007 413 1056. This means the physical address of the L3 table is encoded in the 3rd entry of the L4 table, the physical address of the L2 table is in the 8th entry of the L3 table, the physical address of the L1 table is in the 7th entry of the L2 table, and the physical address of the physical page is at the 267th index of the L1 table. Finally, the byte we are accessing is the 558th byte on the physical page. In a picture, this mapping can be represented as:
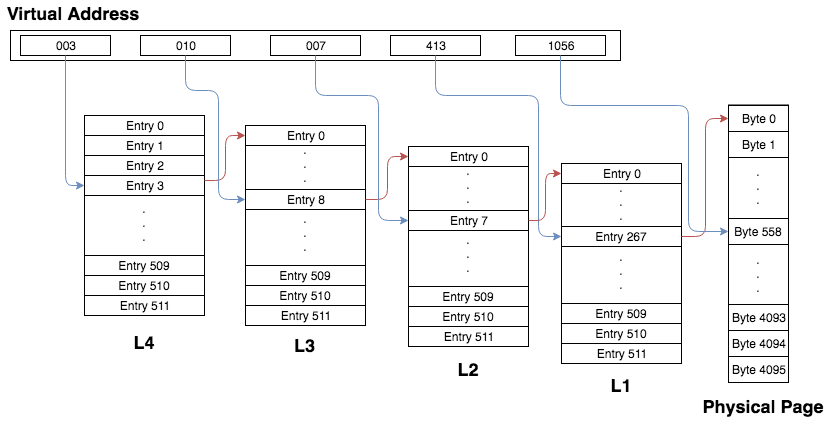
If the operating system had to do this translation every time a program needed to access memory, things would be incredibly slow. Luckily, the processor takes care of performing the virtual to physical address translation in hardware. Intel processors have a special register called cr3 which stores the physical address of the L4 table. From here, the entire translation can be done.
Bit 7 in the entry is 1 if the physical address points to a huge page. There are two huge page sizes – 2 megabytes, or 1 gigabyte. This bit can only be set in L3 or L2. If it’s set in L3, that means the physical address points to a 1 gigabyte page and the bottom 30 bits of the virtual address are an index into that page. Likewise, in the L2 table, this bit being set means the physical address points to a 2 megabyte page and the bottom 21 bits of the virtual address are an index into that page. Theoretically, we could have 512 gigabyte (2^39) pages, but that would require at least 512 gigabytes of physical memory available and would likely never be useful in the foreseeable future. Thus, a large page bit in the L4 is not allowed.
In order to make the translation more efficient, processors have a TLB, or translation lookaside buffer, which caches the virtual to physical address mapping. Since program instructions are also stored in memory (at virtual addresses), there is actually an iTLB (for instructions) and a dTLB (for program data). Furthermore, there is a separate TLB for small and large pages. For known, large blocks of memory, huge pages can be beneficial especially if the TLB miss rate in your program is high. The TLB is independent from the actual data caches (i.e. L1, L2, and L3 caches). Note that the L1, L2, and L3 caches cache virtual addresses, not physical addresses. Thus, having virtual address locality is what matters, regardless of where the physical RAM lies (although one page of physical RAM must be contiguous).
In linux, each process has it’s own virtual address space. This means the 256 terabyte limit discussed earlier is actually a per process limit (although, it is unlikely a process will ever need that much virtual memory in the foreseeable future). One thing virtual memory allows the operating system to do is “create” memory that is not backed by physical RAM. Then, as the memory is accessed, it can find physical memory to back it. Furthermore, if the operating system is out of physical RAM, it can swap a different region of physical RAM to disk and reclaim some RAM. How is this implemented?
If the processor encounters an entry which is not present (bit 0 of the entry is set to 0), it generates a hardware page fault. The operating system can register a handler for the page fault which will be switched into when this fault is triggered. It can then determine (potentially using the OS defined bits in the entry) if the virtual address:
- is backed by disk (i.e. because it’s been swapped)
- has been allocated but does not have a physical frame backing it (in which case a physical page needs to be allocated)
- is inaccessible by the process (in which case Linux will generate a segmentation fault and deliver it to the process).
When an operating system needs to fork a new process, handle a page fault, or create a virtual to physical address mapping, it needs to be able to modify the page tables themselves. The physical address of the page map level 4 table is stored in the cr3 as mentioned earlier, but the problem is the operating system itself must access memory through its virtual address – knowing the physical address is meaningless. One elegant solution to this problem is known as a recursive page table mapping.
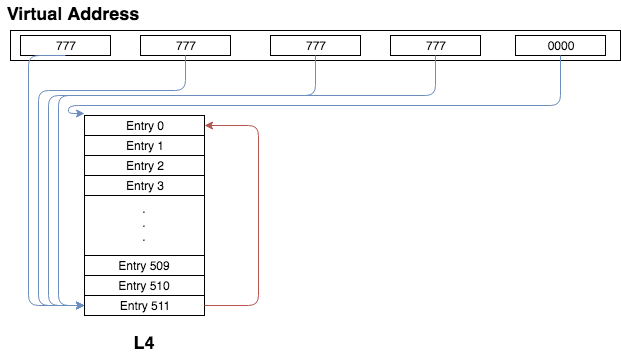
In this scheme, the last entry (i.e. index 511) of the L4 table maps to itself (i.e. the physical address of the start of the L4 table itself). This is nice, because the virtual address (in 48 bit octal) 777 777 777 777 0000 will point to the L4 table. Why? Because the L4 index is 511 (777 in octal), but that entry points to the top of the L4 table (which is now the L3 table). This index is 511, which again points to the top of the L4 table, and so on. In a picture:
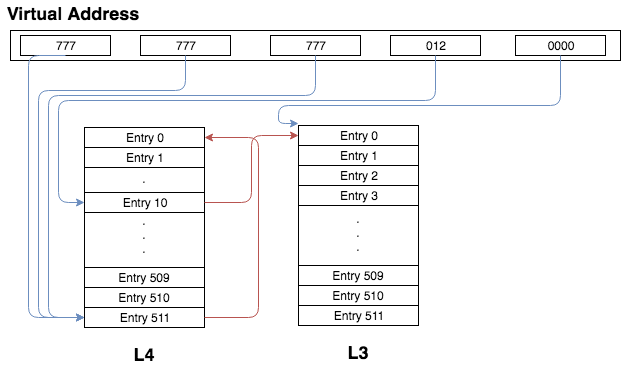
What’s interesting about this, is the L3 table for the ith entry can be accessed by changing the rightmost 777 to i. For example, the address 777 777 777 012 0000 will point to the L3 table of the 10th (012th in octal) entry (i.e. that is the virtual address for the physical address in the 10th entry of the L4 table). Why? The first 3 777s all points back to the L4 table. The 012 points to the 10th entry, which has a physical address of an L3 table. This is treated as a physical page and our index into that is 0, so we get a pointer to the top of the L3 page. Again, a picture is worth a thousand words:
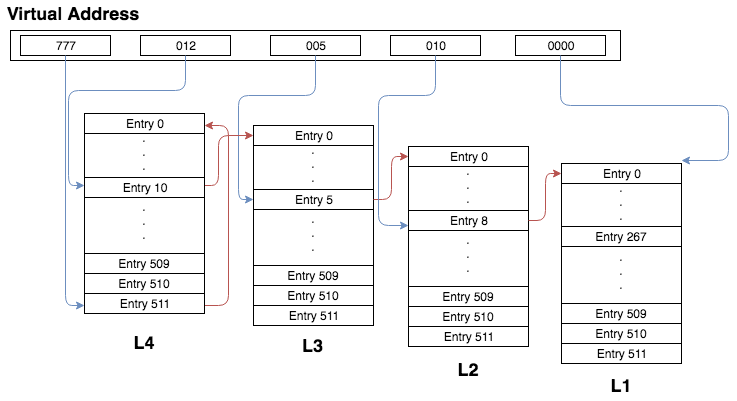
We can take this one step further and access the L2 page of the 5th entry of the L3 page pointed to by the 10th entry of the L4 page by again shifting the virtual address up by 4 and oring by the entry index (in this case 5). This gives us the address 777 777 012 005 0000. As above, the first two 777s get us back to the L4 table. The 012 puts us at the L3 page for the 10th entry of the L4 page. 005 will get us to the L2 page pointed to by the second entry of the L3 page we were just at. The picture below illustrates this by going another step further and accessing one particular L1 page:
At this point, we have covered the essentials of virtual memory, one of the fundamental building blocks of Linux (or any OS for that matter). In subsequent posts, we will dive further by exploring virtual addressing as it pertains to Linux and maybe even implementing our own virtual memory manager for a toy OS.